编译器优化了什么

时间：2024-05-26 09:47:27

[经 @污博士提醒，我决定把题目改了…]

最近在做一个 x86 到 x86 的 jit 编译器，因之前大多接触的是编译器前端知识，所以重新学习了一遍中后端原理，做个整理，也欢迎交流拍砖。

这里不打算涉及具体的工程细节，只在抽象的整理一下程序的优化空间在哪里。文章不是很正式，不要拘泥于命名。。

编译器最基本的工作就是把源语言翻译成目标语言并保证所表达的内容相同，简单拆分一下，前端将源语言翻译成中间表示，后端将中间表示翻译成目标语言。在大多数时候前端的翻译并不关心执行效率，也就是不做优化。

中间表示本身也是一种描述性的语言，包含了程序的全部信息，举个栗子：

a=b + c + d;

中间表示一般有两种形式，树：

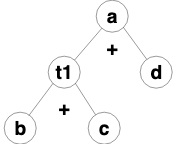
或者展开的序列表示：

t1=b + c;
a=t1 + d;

那为什么要中间表示呢？

为了复用，中间表示抽象了不同语言（包括不同源语言和目标语言）编译过程中的公共部分。良好定义的中间表示极大的方便了新语言的发明，比如 llvm。
为了方便优化。

终于要进入正题了。编译的最基本要求其实就是两种不同语言所表达的内容是等价的，或者具体一点就是计算结果是一致的。虽然上面没有具体展开（后面会有具体的说明），但应该很明显这两种中间表示和源语言是等价的，为简单起见，这里我们就当中间语言的序列表示就是编译结果吧。。

而其实对于一段源语言代码来说，在保证等价的基础上，可以有很多种不同的翻译，所谓优化就是在里面找一种最好的结果。比如对于上面的栗子，结果还可以是：

t1=c + d;
a=b + t1;

这有啥区别，看起来是不一样了，但好像没有哪个更好嘛。在这之前，我们需要定义一下什么算更好，两种最一般的就是执行更快，或者内存使用更少。对应到这里，就是行数更少，或者涉及的符号更少，所以确实，呃，确实是一样的。然而结果还可以是：

t1=c + d;
t2=t1 + 0;
a=b + t2;

嗯，有点耍流氓的感觉，这样的话结果就变成无穷多的了，但这里确实可以作为一个解释哪个更好的栗子，因为在我们的不管哪个定义下，这个都没之前两个好（否则我们就没法得到最好的结果了。。）。不过再多做一些解释，比如对于 x86 插入 nop 在一些时候确实是一种优化手段，它可以使后面的指令对齐，提高缓存效率。

好了，光看这个定义，我们就可以尝试（粗暴的）实现一个最简单的编译器了。遍历所有的指令组合，剪掉行为不一致的，剪掉含无用操作的，然后从里面挑一个最好的。当然这个在现实中是不可行的，因为实在太慢了。（而且深究的话，我想这两个剪枝应该也是难以实现的。）

2.0 static single assignment

这么粗暴的搜索是不可行的。看来我们需要一个考虑领域知识的搜索，或者不是搜索的方案。

是时候稍更正式的解释一下上面给出的中间表示，比如上面这棵树为什么长这样。好吧，还是要先说一下它到底长成什么样了：

每个节点下面（最多）只有两个节点
父节点的值直接依赖子节点的值
相同的名字不出现两遍

这大体上就是所谓的 static single assignment 的定义。

所以为什么长这样呢。在这之前先确定一下这样确实能解决问题，比如目标语言还是上面的序列语言，具体的说每一行只能有两个输入变量和一个输出变量，也就是 z=x op y，从树表示到结果，我们只要先子节点的遍历整棵树，在每个节点上输出一行对应的操作语句就好了。

所以为什么长这样，为什么不长成：

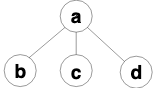
看一个更复杂的栗子：

a=x + y + z;
b=x + y;
c=a + b;

对于 c 的结果来说可以很明显的看到 x + y 在计算 a 和 b 的时候重复了，也就是所谓的公共子表达式。有理由相信我们可以得到：

t1=x + y;
t2=t1 + z;
c=t1 + t2;

所以：

如果中间表达长这样：

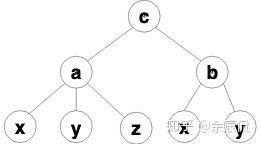
我们很难从这个表示中找到公共子表达式，使用二叉的形式可以在最细的粒度上找到重复表达式。（怎么方便的在二叉里面找子表达式？全量的方法是遍历整棵树，子节点相同的两棵子树就是公共子表达式，当然合并以后树就变成单向图了。）

同时如果我们在第二行重复使用了 t1 的名字，前两行变成：

t1=x + y;
t1=t1 + z;

于是要用的公共子表达式结果被我们顺利的干掉了。。

a=1 + 2 + b;

结果：

a=3 + b;

这个在树上做很容易，先子节点的遍历，将能计算的计算了就好了。所以被称为折叠，也就是把一整棵子树折叠进一个节点里。

如果已经有了树，根节点就是最终的计算结果，最终没有连到树上的就是对结果无关的代码。除了释放内存以外，删除这个不需要额外的操作。。

上面这些优化好像没什么选择的问题，那所以选择最优结果的过程在哪儿？有几个方面，比如：

遍历的顺序，对于一个树或者图表达的中间形式，要最终得到有序的目标代码，有很多不同的遍历方式，而唯一要遵守的规则就是先遍历子节点。
目标代码（指令）的选择，对于每一条形如 z=x op y 的中间代码，目标代码至少在几个方面有灵活的选择空间，比如 x y z 放在哪儿，寄存器还是内存，op 用具体哪个操作等。

下一个问题是为什么这些选择对最终结果有影响。简单的说这有点像小时候的应用题，比如怎么在有限资源下安排一堆有各种要求，又互相依赖的任务，比如最终的目标是做一桌菜，要烧水，要洗菜，切菜，然后有两个锅，有一个烤箱，怎么样能最快的把一桌菜做好。而在这里，寄存器数量是有限的，但还是可选的，有内存，但比较慢，有多个计算单元，所以希望尽可能多的不让这些单元空闲。

这里主要是为了说明优化空间，不太多涉及具体怎么优化，一般的说，没法在多项式复杂度的时间里找出最优结果，对于启发式的策略，就举一个寄存器相关的栗子：

a=f () + g ();

比如这里，应该先计算 f () 还是 g ()，一个策略是先计算需要用到更多寄存器的子表达式，这样它的计算结果更有可能被保持在寄存器里（当然这里不涉及函数的调用惯例，所以不假设有固定数量的寄存器会被使用或者保留）。具体的说，比如一共两个寄存器 a 和 b，f () 需要用到一个寄存器，g () 用到两个，按照这个策略应该先计算 g ()，这样结果保留在 a 中，而让 f () 使用寄存器 b，就不需要把计算结果放到内存中了。

a=b + c;

然而到现在为止，如果不是脱离实际，优化至少也是完全不完整的，这种形式的表达式离最简单的程序都很遥远，因为程序显然不只有表达式，而 b 和 c 又没解释是从哪里来的。

比如控制语句：

x=y + z;
if (y)
  b=p + x;
  a=b + c;
else
  a=c + d;

上面的优化的确只能优化表达式，不过像上面第三第四行的两个语句，对结果 a 来说实际可以理解为一个表达式，即 a=p + x + c;，而像这样的一串不含分支的语句被称为基本块，上面所说的优化就是在这个基础上执行的。

但完全将基本块独立出来处理显然还有很多的优化空间，因为这样处理丢失了跨基本块的可用信息，比如上面的 x 值可能是已知的，但如果把三四行独立出来优化的话这个信息就丢失了。

有几种方式解决这个问题：

放大基本块的范围，比如将上面的代码处理成：

b1:
  x=y + z;
  if (! y) goto b2;
  b=p + x;
  a=b + c;

b2:
  a=c + d;

这样对于 b1 来说，x 值的信息就被保留下来了。

数据流分析，简单说就是在基本块间追踪数据范围，比如对：

b1:
  x=1;
  goto b3;

b2: 
  x=2;
  goto b3;

b3:
  a=x <=2;

我们可以在基本块之间追踪 x 的值，这样我们就可以把 b3 优化成 a=1;。

当追踪不了的时候只要按照最保守的范围进行优化就能保证程序正确性。同时这也可以用于程序静态分析，比如未初始化变量的分析。

数据流分析可以对各种数据进行分析，比如在变量有别名（比如指针）的时候，纯粹的数值分析就会有问题，因为你并不知道指针会指向哪儿，这个时候就可以对指针所指的目标做数据流分析，继而对对应的数值进行分析。

具体的技术实现细节参考《编译原理》，《编译器设计》。。。

编译器优化了什么

电话：